Intersectia graficului cu axele

Pe langa varful graficului, urmatoarele puncte la care ar trebui sa ne uitam sunt intersectia cu axele.

Intersectia cu $O y$ $Oy$

Intersectia cu axa $O y$ $Oy$ este punctul de coordonate $(0, f (0))$ $(0, f(0))$

Asa ca pentru o functie de gradul II de forma

$f (x) = a \cdot x^{2} + b \cdot x + c$ $f(x)=a*x^2 + b*x + c$

daca inlocuim $x$ $x$ cu $0$ $0$ , ne va ramane doar termenul liber

$f (0) = a \cdot 0^{2} + b \cdot 0 + c = c$ $f(0) = a*0^2 + b*0 + c = c$

Asadar, intersectia cu axa $O y$ $Oy$ este data de termenul liber, si va avea forma $(0, c)$ $(0, c)$ .

Exemple

De exemplu, daca avem functia $f (x) = x^{2} + 4 \cdot x + 4$ $f(x) = x^2 + 4*x + 4$

Atunci $f (0) = 0^{2} + 4 \cdot 0 + 4 = 4$ $f(0) = 0^2 + 4*0 + 4 = 4$ . Iar punctul de intersectie va avea coordonatele $(0, 4)$ $(0, 4)$ .
$f (x) = 2 \cdot x^{2} - 7$ $f(x) = 2*x^2 - 7$

$f (0) = 2 \cdot 0^{2} - 7 = - 7$ $f(0) = 2*0^2 - 7 = -7$ atunci punctul va avea coordonatele $(0, - 7)$ $(0, -7)$
$f (x) = \frac{1}{3} \cdot x^{2} + 4 \cdot x$ $f(x) = 1/3*x^2 + 4*x$

$f (0) = \frac{1}{3} \cdot 0^{2} + 4 \cdot 0 = 0$ $f(0) = 1/3*0^2 + 4*0 = 0$ iar punctul va fi $(0, 0)$ $(0, 0)$ pentru ca $c = 0$ $c=0$

Intersectia cu $O x$ $Ox$

O functie de gradul II va intersecta intodeauna axa $O y$ $Oy$ , dar nu este sigur ca va o intersecta si pe $O x$ $Ox$ .

Intersectia cu $O x$ $Ox$ este atunci cand $y = 0$ $y = 0$ . Adica atunci cand:

$a \cdot x^{2} + b \cdot x + c = 0$ $a*x^2 + b*x + c = 0$

Asadar intersectia cu axa $O x$ $Ox$ reprezinta solutia ecuatiei de gradul II.

Dar stim ca o ecuatie de gradul II nu are intodeauna solutii, de aceea este posibil ca acea functie sa nu intersecteze axa $O x$ $Ox$ .

De exemplu, daca avem functia:

$f (x) = x^{2} - x - 2$ $f(x) = x^2 - x - 2$

Pentru a afla solutiile ecuatiei trebuie sa calculam $Δ$ $Delta$ , care va fi:

$Δ = {(- 1)}^{2} - 4 \cdot a \cdot (- 2) = 1 + 8 = 9 > 0$ $Delta = (-1)^2 - 4*a*(-2) = 1+8=9 > 0$

Pentru ca $Δ > 0$ $Delta > 0$ inseamna ca vom avea doua solutii, iar acestea vor fi $x_{1} = 2$ $x_1 = 2$ si $x_{2} = - 1$ $x_2 = -1$ , ceea ce inseamna ca vom avea punctele de coordonate $(2, 0)$ $(2, 0)$ si $(- 1, 0)$ $(-1, 0)$ , lucru care se vede si din graficul functiei:

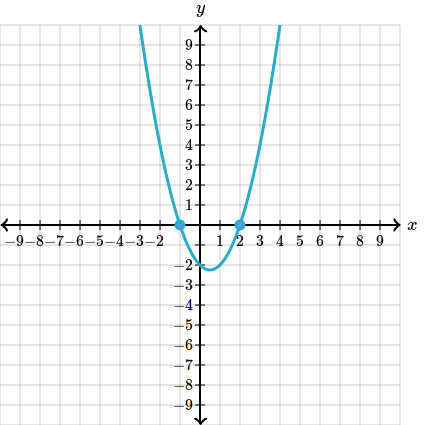
$Intersectia cu axa Ox$

Asadar $Δ$ $Delta$ este cel care ne spune cate puncte de intersectie are graficul cu axa $O x$ $Ox$ .

Aceasta inseamna ca ne putem folosi de el pentru a afla din timp daca graficul intr-adevar va intersecta axa $O x$ $Ox$ :

$Δ > 0$ $Delta > 0$
$Δ = 0$ $Delta = 0$
$Δ < 0$ $Delta < 0$

Intersectia cu OyOyOy

Exemple

Intersectia cu OxOxOx

Intersectia cu $O y$ $Oy$

Intersectia cu $O x$ $Ox$