Varful graficului

Varful graficului este punctul extrem al oricarui grafic pentru o ecutie de gradul 2.

Daca luam de exemplu, functia din lectia trecuta:

$f (x) = \frac{1}{3} \cdot x^{2} + 2 \cdot x - 5$ $f(x) = 1/3*x^2 + 2*x - 5$

Varful graficului va fi punctul cel mai de jos. In acest caz are coordonatele $(- 3, - 8)$ $(-3, -8)$

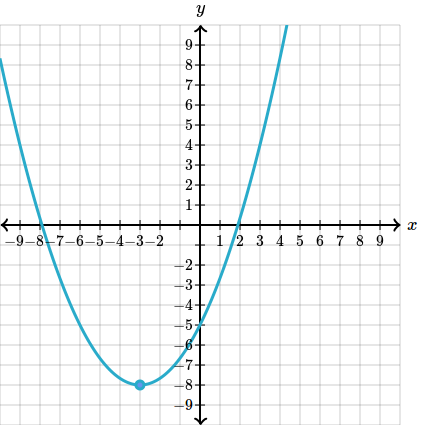
Acest punct este punctul minim al graficului deoarece coeficientul lui $x^{2}$ $x^2$ este mai mare ca $0$ $0$ . Acest lucru face ca acest grafic sa fie covex, sau altfel spus cu ramurile in sus.

Daca acel coeficient ar fi negativ atunci, vom avea o functie complet diferita:

$f (x) = - \frac{1}{3} \cdot x^{2} + 2 \cdot x - 5$ $f(x) = -1/3*x^2 + 2*x - 5$

Iar graficul ei ar arata rasturnat:

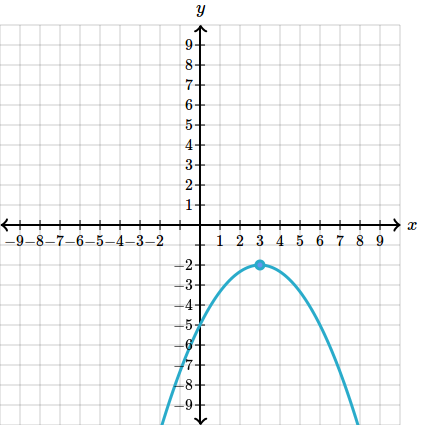
In acest caz varful graficului nu mai este punctul minim, ci este punctul maxim, si are coordonatele $(3, - 2)$ $(3, -2)$ . Acest grafic se numeste concav.

Calcularea varfului

Indiferent de unde situat varful graficului, ii putem afla coordonatele folosind aceeasi formula

Formula de calcul pentru coordonatele varfului unui grafic, pentru functia de gradul II este:

$V (- \frac{b}{2 \cdot a}, - \frac{Δ}{4 \cdot a})$ $V (-b/(2*a), -Delta/(4*a))$

$Δ$ $Delta$ stim din calcularea ecuatiei de gradul II, ca are urmatoarea formula:

$Δ = b^{2} - 4 \cdot a \cdot c$ $Delta = b^2 - 4*a*c$

unde $a$ $a$ , $b$ $b$ si $c$ $c$ sunt coeficientii ecuatiei.

Exemple

Haideti sa luam cateva exemple de functii de gradul 2 pentru care sa calculam coordonatele varfului

$f (x) = 2 \cdot x^{2} + x + 3$ $f(x) = 2*x^2 + x + 3$

Coeficientii sunt $a = 2$ $a=2$ , $b = 1$ $b=1$ si $c = 3$ $c=3$ .

$a > 0$ $a > 0$ asta inseamna ca graficul functiei va fi convex si va semana cu graficul primei functii din lectie.

Coordonatele varfului vor fi:

$V (- \frac{1}{2 \cdot 2}, - \frac{1^{2} - 4 \cdot 2 \cdot 3}{4 \cdot 2}) = V (- \frac{1}{4}, - \frac{23}{8})$ $V(-1/(2*2), -(1^2-4*2*3)/(4*2) ) = V(-1/4, -23/8)$
$f (x) = - x^{2} - 4 x + 1$ $f(x) = -x^2 - 4x + 1$

Coeficientii sunt $a = - 1$ $a=-1$ , $b = - 4$ $b=-4$ si $c = 1$ $c=1$ .

Pentru ca $a < 0$ $a < 0$ atunci graficul functie va fi rasturnat cu ramurile indreptate in jos, numit si concav.

Coordonatele varfului vor fi:

$V (- \frac{1}{2 \cdot 2}, - \frac{1^{2} - 4 \cdot 2 \cdot 3}{4 \cdot 2}) = V (- \frac{1}{4}, - \frac{23}{8})$ $V(-1/(2*2), -(1^2-4*2*3)/(4*2) ) = V(-1/4, -23/8)$

Indiferent daca este punctul minim sau punctul maxim, varful graficului reprezinta punctul extrem al oricarui grafic. De aceea merita atentie speciala si o formula de calcul.