Despre grafic

Ca si in cazul functiei lineare, putem reprezenta grafic o functie de gradul II.

Acest grafic are o forma speciala si poarta denumirea de parabola.

De exemplu, functia $f (x) = \frac{1}{3} \cdot x^{2} + 2 \cdot x - 5$ $f(x) = 1/3*x^2 + 2*x - 5$ , va avea urmatorul grafic:

Vedem ca nu seamana deloc cu graficul functiei de gradul I. In acel caz aveam o simpla dreapta.

Punctele de pe grafic

In acest caz (ca si pentru orice alta functie), graficul reprezinta toate perechile de numere ce rezulta din functia noastra.

De exemplu, daca inlocuim $x$ $x$ cu $3$ $3$ in $f (x)$ $f(x)$ ne va rezulta:

$f (3) = \frac{1}{3} \cdot 3^{2} + 2 \cdot 3 - 5 = 4$ $f(3) = 1/3*3^2 + 2*3 - 5 = 4$

Aceasta inseamna ca perechea de numere $(3, 4)$ $(3, 4)$ reprezinta o solutie pentru functia noastra si in acelasi timp este si un punct pe acest grafic:

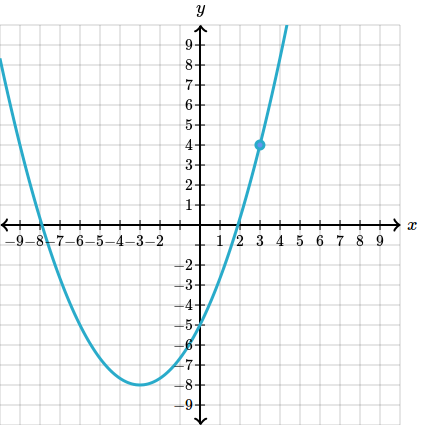
Asadar, fiecare punct de pe aceasta linie va avea doua coordonate, si daca le vom inlocui in ecuatia functiei ne va da o egalitate.

Cine influenteaza graficul functiei

Coeficientii lui $x$ $x$ din ecuatia functiei influenteaza cum arata aceasta. Fiecare o influenteaza intr-un mod anume, asa ca haideti sa vedem cum:

Daca $a > 0$ $a > 0$ atunci graficul este indreptat in sus (precum mai devreme). Acest grafic se numeste convex. Daca $a < 0$ $a < 0$ atunci graficul este indreptat in jos, numit si concav.

$a > 0$ $a > 0$
$Grafic convex$

$a < 0$ $a < 0$
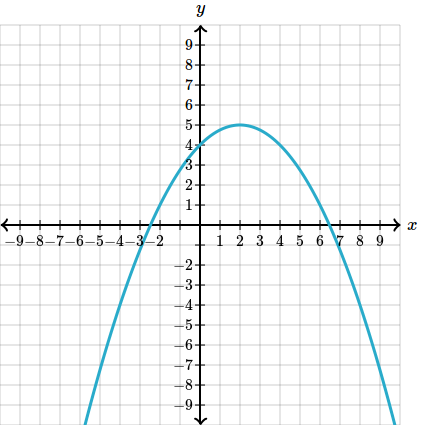
$Grafic concav$
Coeficientul $c$ $c$ ne arata punctul de intersectia cu axa $O y$ $Oy$ . Vedem in exemplele de mai sus ca in stanga avem $c = - 5$ $c = -5$ iar in dreapta avem $c = 4$ $c=4$ .
Coeficientul $b$ $b$ ne arata cat de departe este varful graficului (in stanga, punctul cel mai de jos) de locul unde graficul intersecteaza axa $O y$ $Oy$ .

In lectiile urmatoare ne vom axa pe cateva puncte mai speciala, si anume vom discuta despre varful graficului si despre intersectia cu axele. Abia apoi vom discuta de restul punctelor, in mod general.

Vom incepe cu varful graficului care in cazul de mai sus este punctul minim al lui.