Diferenta dintre doi vectori

Diferenta dintre doi vectori se poate afla destul de simplu folosind sistemul de axe.

De exemplu daca avem urmatorii doi vectori `vec a` si `vec b`:

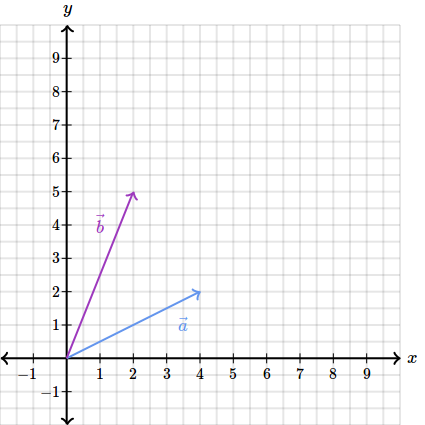
Atunci diferenta dintre cei doi, si mai exact `vec a - vec b` va fi vectorul `vec c`:

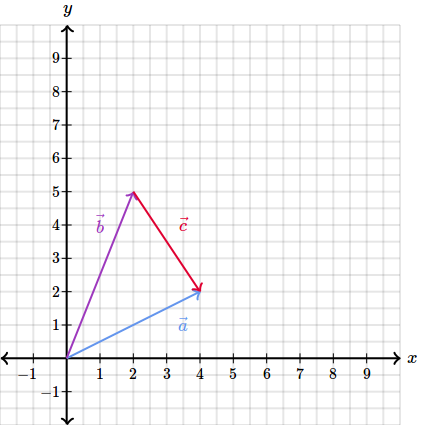
Vedem ca atunci cand calculam diferenta vom uni extremitatea celui de-al doilea vector (in acest caz `vec b`) cu cea a primului (adica `vec a`).

Daca vrem sa calculam `vec b - vec a` atunci ne va rezulta `vec d`:

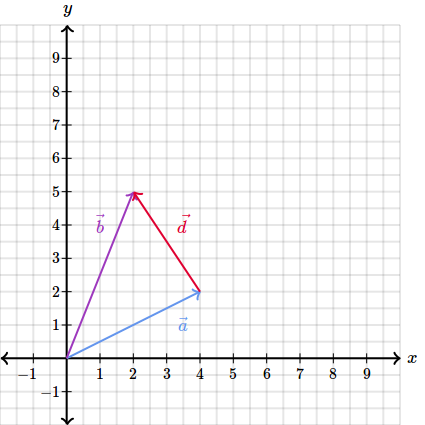
Care vedem ca este opusul lui `vec c`.

Deci vectorul care va rezulta, va uni al doilea vector cu primul.

De ce?

Un mod de a intelege acest rezultat este sa ne gandim la diferenta dintre doi vectori drept o suma:

`vec a - vec b = vec c => vec a = vec b + vec c`

Daca este sa privim `vec a` drept rezultatul dintre `vec b` si `vec c` atunci ne e simplu sa gasim `vec c` care sa completeze acea suma:

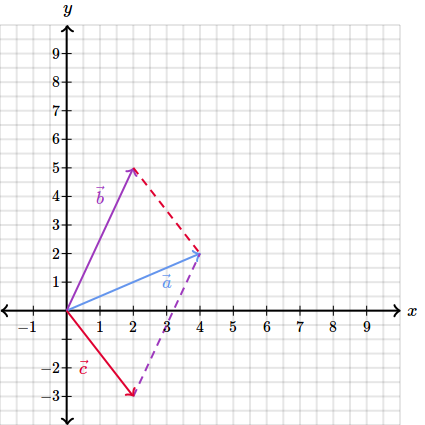
Asadar, noi trebuie sa gasim `vec c` astfel incat `vec b + vec c = vec a`. Si apoi acel vector va fi mutat astfel incat sa uneasca extremitatile vectorilor care se scad.

O alta metoda este sa ne imaginam ca `vec a - vec b = vec a + (- vec b)`.

Asadar avem primul vector adunat cu opusul celui de-al doilea, iar grafic ar arata astfel:

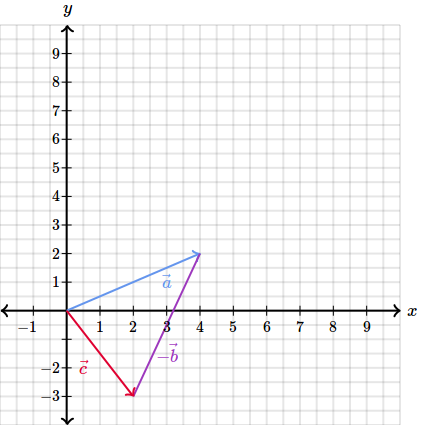
In suma vom uni punctul de start al primului vector cu extremitatea celui de-al doilea, si ne va rezulta acelasi vector `vec c`.

Calculul matematic

Putem bineinteles afla diferenta dintre vectori si matematic.

De exemplu, pentru vectorii de mai devreme avem `vec a = [[4], [2]]` si `vec b = [[2], [5]]`, atunci:

`vec a - vec b = [[4], [2]] - [[2], [5]] = [[2], [-3]]`

Si daca ne uitam la `vec c`, vedem ca el chiar se deplaseaza `2` unitati la dreapta si `3` in jos, adica `[[2], [-3]]`.