Sisteme de inecuatii lineare

Daca intalnim cel putin $2$ $2$ inecuatii lineare intr-o situatie, atunci avem un sistem de inecuatii lineare.

Solutia fiecarei inecuatii va fi o regiune din sistemul de axe, dar solutia sistemului va fi partea din grafic care este comuna ambelor inecuatii (daca exista).

Sa spunem ca avem inecuatia:

$\frac{1}{2} \cdot x + 3 \leq y$ $1/2*x + 3 ≤ y$

care are urmatorul grafic:

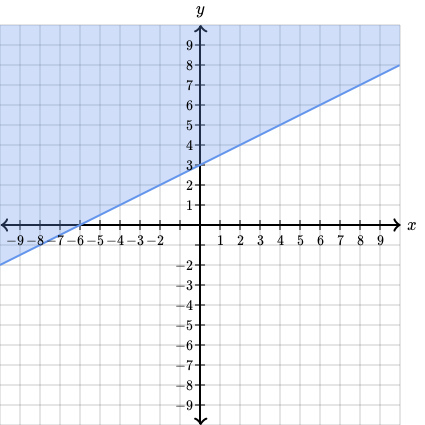
Si inecuatia:

$- x + 2 \leq y$ $-x + 2 ≤ y$

care are graficul:

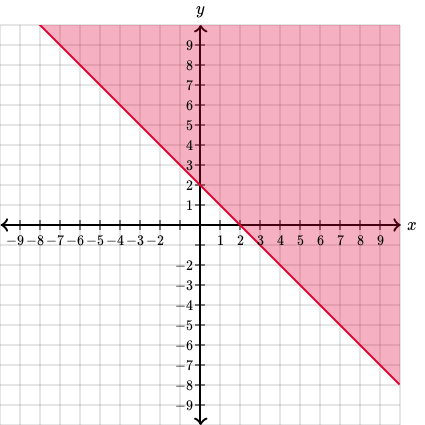
Iar impreuna, formeaza sistemul:

{\begin{cases} 1 / 2 \cdot x + 3 \leq y \\ - x + 2 \leq y \end{cases}

$\begin{cases} \class{text-blue}{1/2 \cdot x + 3 \le y} \\ \class{text-red}{-x + 2 \le y} \end{cases}$

Si cum am spus mai devreme, solutia acestui sistem va fi regiunea de intersectie a celor doua grafice:

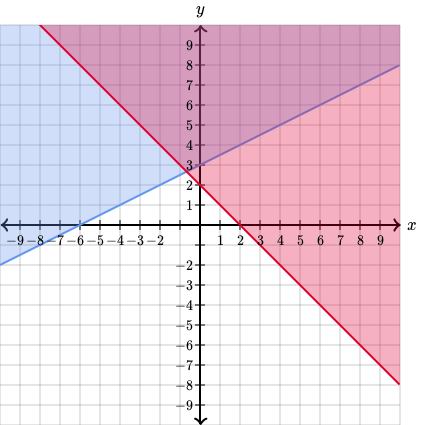
Adica acea regiune care este cuprinsa in ambele grafice, care are culoare apropiata de mov.

Cand este folositor acesta?

De obicei astfel de lucruri se folosesc in economie. Atunci cand vrei sa gasesti ce anume poti sa faci cu o suma de bani. Sau chiar in cazul unei persoane, atunci cand ai o suma de bani si vrei sa stii cum o poti cheltui.

Sa spunem ca ai primit o suma de bani, 45 lei mai exact, pe care poti sa o cheltui doar pe un site anume. Acel site ofera reduceri pentru jocuri online, care costa $3$ $3$ lei fiecare si melodii, care costa $4, 5$ $4,5$ lei.

Pentru a obtine aceste preturi trebuie sa cumperi cel putin 10 lucruri din acesti bani, nu conteaza daca sunt jocuri sau melodii.

Cum poti folosi inegalitatile pentru a vedea (grafic) care sunt optiunile tale de cumparare?

Putem sa notam numarul de jocuri pe care am putea sa la cumparam cu $g$ $g$ si numarul de melodii cu $m$ $m$ . Iar pentru ca vrem sa cumparam cel putin $10$ $10$ lucruri, avem prima inegaltiate:

$g + m \geq 10$ $g + m >= 10$

Stim costul pentru fiecare, si suma totala. Putem a crea a doua inegaltiate folosindu-ne de acestea si de numarul de lucruri pe care vrem sa le cumparam:

$3 \cdot g + \frac{1}{2} \cdot m \leq 15$ $3*g + 1/2*m ≤ 15$

Asadar avem sistemul:

${\begin{cases} g + m \geq 10 \\ 3 \cdot g + \frac{9}{2} \cdot m \leq 45 \end{cases}$ ${(g + m >= 10), (3*g + 9/2*m ≤ 45):}$

Si putem incepe prin reprezentarea grafica a primei inecuatii. In acest caz, putem sa ne imaginam ca $y$ $y$ sa fie $g$ $g$ , sau $m$ $m$ . Nu conteaza foarte mult. Asadar, inecuatia scrisa in functie de $g$ $g$ va fi: $g \geq 10 - m$ $g >= 10 - m$ . Care va avea graficul:

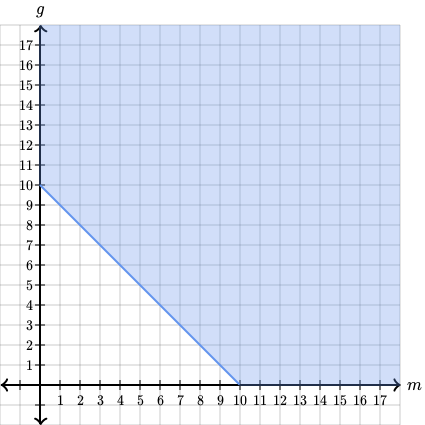
Vom folosi un sistem doar cu numere pozitive, pentru ca nu avem cum sa cumparam $- 2$ $-2$ melodii. Sau matematic vorbind, functiile care au aceste ecuatii sunt definite pe multimea $[0, + \infty)$ $[0, +infty)$ cu valori in $[0, + \infty)$ $[0, +infty)$ .

A doua inecuatie, dupa ce vom lasa $g$ $g$ in partea stanga si vom inmultii cu $\frac{1}{3}$ $1/3$ , va avea forma $g \leq 15 - \frac{3}{2} \cdot m$ $g ≤ 15 - 3/2*m$ . Care va avea graficul urmator:

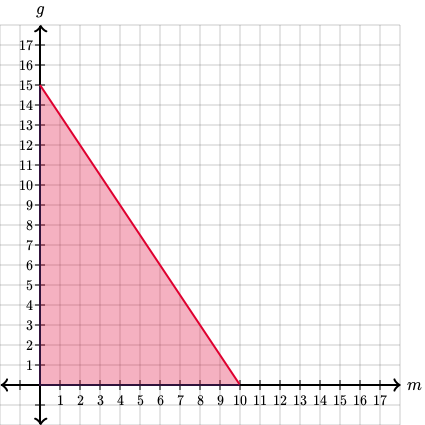
Iar impreuna, graficele celor doua inecuatii vor avea aceasta regiune in comun:

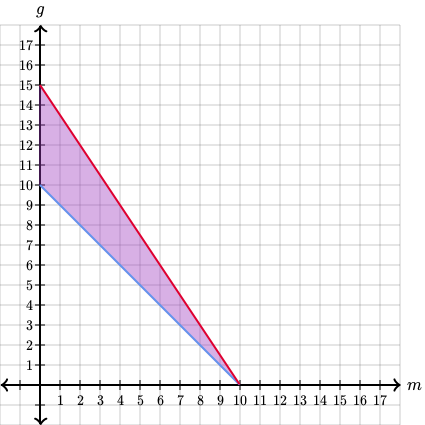
Iar fiecare punct din aceasta regiune, este o optiune de cumparare.

De exemplu, vedem ca in regiune se afla punctul de coordonate $(3, 8)$ $(3,8)$ . Aceasta inseamna ca putem cumpara $3$ $3$ melodii si $8$ $8$ jocuri (in total $11$ $11$ obiecte digitale) si ne va mai ramane si un rest

$3 \cdot 8 + \frac{9}{2} \cdot 3 = 37.5 < 45$ $3*8 + 9/2*3 = 37.5 < 45$ lei.

Dar pentru a cheltui (cat mai "complet") banii trebuie sa ne apropiem foarte mult de dreapta rosie. Cu cat un punct va fi mai aproape de ea, cu atat ne vor ramane mai putini bani.

De fapt, cea mai buna optiune este sa alegem un punct care se afla pe dreapta. Acesta inseamna ca vom consuma complet suma de bani. Pe dreapta rosie avem punctele:

$(0, 15), (2, 12), (4, 9), (6, 6), (8, 3), (10, 0)$ $(0, 15), (2, 12), (4, 9), (6, 6), (8, 3), (10, 0)$

am folosit doar numere naturale pentru ca nu putem cumpara jumatate din joc.

Asadar, aceste puncte ne arata cele mai bune optiuni de a cheltui banii, iar acum nu trebuie decat sa ne decidem care din aceste optiuni o dorim. Adica ce numar de melodii si jocuri dorim. Primul numar din coordonatele punctelor, reprezinta numarul de melodii, iar al doilea numarul de jocuri.

Astfel de sisteme se pot face in diverse momente de acest gen. Cand exista mai multe variabile si vrem sa vedem ce optiuni avem si mai exact, care este cea mai buna optiune. Dar economia, nu este singurul domeniu in care putem aplica acest gen de calcul.