Adunarea a doi vectori

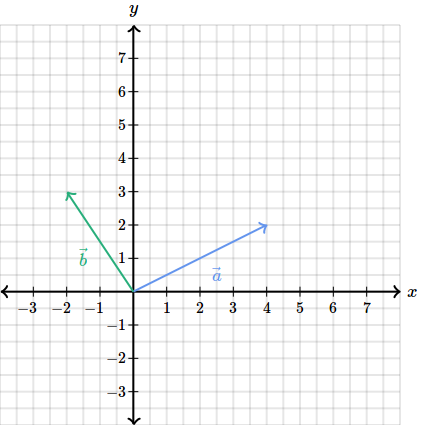
Am vorbit despre ce este un vector si cum se reprezinta dar ce se intampla de fapt cand vrem sa adunam doi vectori?

Daca ne avem doi vectori, sa spunem `vec a = [[4], [2]]` si vectorul `vec b = [[-2], [3]]` atunci suma celor doi ar insemna sa adunam numerele care sunt pe acelasi rand:

`vec a + vec b = [[4], [2]] + [[-2], [3]] = [[2], [5]]`

Ne aducem aminte ca numarul de sus arata cat de mult un vector se duce la dreapta, pe axa `Ox` (sau daca este negativ, la stanga) iar numarul de jos, cat de mult de duce in sus, pe axa `Oy`.

Iar rezultatul va fi un nou vector care va respecta coordonatele `[[2], [5]]`:

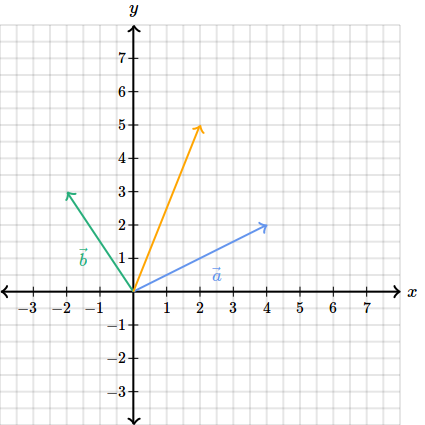
Cand calculam suma a doi vectori nu trebuie neaparat sa incepem din origine, dar e mai simplu de vizualizat daca facem asta.

Metoda grafica

Chiar daca nu stim dimensiunile unui vector ne putem folosi doar de grafic si de sistemul de axe pentru a aduna doi vectori.

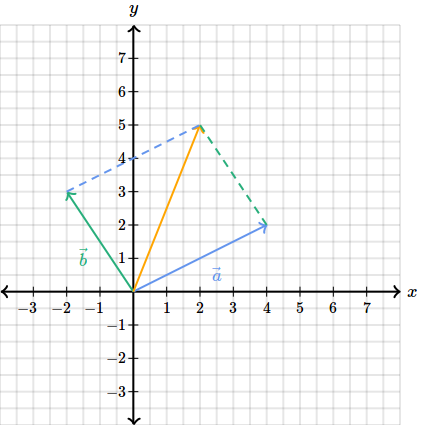
O metoda simpla este sa pornim cu un vector, sa spunem `vec b` si apoi la finalul lui (in punctul lui extrem) sa continuam cu `vec a`. Apoi daca unim originea cu punctul final ne va da rezultatul sumei:

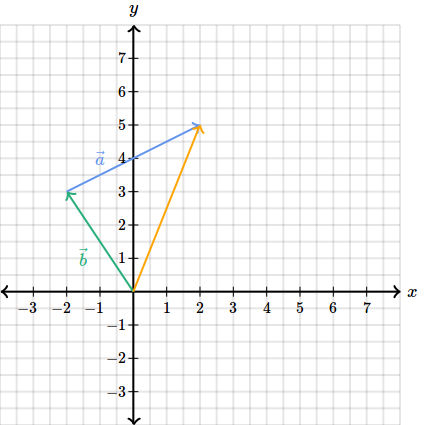
Bineinteles ca am putea sa incepem si cu `vec a`, am obtine acelasi lucru.

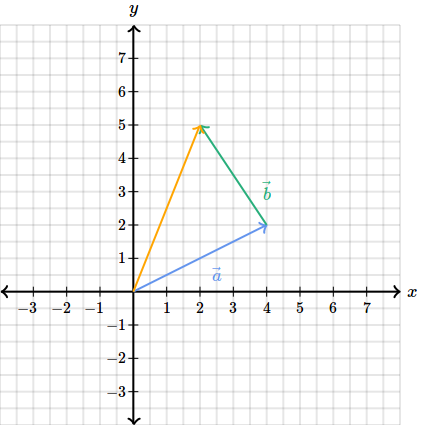
Aceasta metoda se numeste metoda triunghiului pentru ca in final vedem ca ne rezulta un triunghi.

O alta metoda de a reprezenta o suma este metoda paralelogramului. Cu aceasta vom adauga doua linii paralele cu vectorii initiali din care ne va rezulta un paralelogram:

Proprietatile adunarii

Avem si cateva proprietati ale adunarii intre vectori: