Inecuatii de gradul I

Pentru o functie de gradul I precum $f (x) = 7 \cdot x + 8$ $f(x) = 7*x + 8$ , putem crea o inecuatie de forma $7 \cdot x + 8 \geq 0$ $7*x + 8 ≥ 0$ (sau $\leq 0$ $≤ 0$ ).

Aceasta inecuatie nu este altceva decat expresia functiei pentru care vrem sa calculam valorile lui $x$ $x$ , care ne spun locurile unde functia este mai mica sau mai mare decat $0$ $0$ . Si cand spunem ca functia este mai mare decat $0$ $0$ , inseamna ca ne returneaza numere pozitive.

De ce?

Motivul principal pentru a crea inecuatia din expresia unei functii este de a afla mai multe detalii despre functie. Mai exact, putem afla pentru ce valori ale lui $x$ $x$ functia va fi mai mare sau mai mica decat $0$ $0$ .

Nu trebuie neaparat sa facem acest lucru, ci doar daca ni se cere sau daca ne intereseaza in mod special sa aflam pe ce interval functia returneaza valori pozitive sau negative.

Ne putem imagina de fapt, ca orice inecuatie (de forma $a \cdot x + b \geq 0$ $a*x + b >= 0$ ) are o functie atasata, si atunci cand o rezolvam, aflam ceva despre functia care are aceeasi expresie.

Cum calculam?

Rezolvarea se face in modul normal de calcul a unei inecuatii. Interpretarea e apoi mai interesanta.

De exemplu sa spunem ca avem functia:

$f (x) = \frac{3}{2} \cdot x - \frac{4}{5}$ $f(x) = 3/2*x - 4/5$

si vom calcula pentru aceasta functie, cand ecuatia ei este mai mare decat $0$ $0$ , si anume:

$\frac{3}{2} \cdot x - \frac{4}{5} \geq 0 \Rightarrow$ $3/2*x - 4/5 >= 0 rArr$

$\frac{3}{2} \cdot x \geq \frac{4}{5} ∣ \cdot 2 \Rightarrow$ $3/2*x >= 4/5|*2 rArr$

$3 \cdot x \geq \frac{8}{5} ∣ \cdot \frac{1}{3} \Rightarrow$ $3*x >= 8/5|*1/3 rArr$

$x \geq \frac{8}{15}$ $x >= 8/15$

Si ne rezulta ca functia $f (x)$ $f(x)$ este mereu mai mare decat $0$ $0$ cand $x \geq \frac{8}{15}$ $x >= 8/15$ .

Asadar, $\frac{8}{15}$ $8/15$ este punctul dupa care functia ne va returna doar valori pozitive. Si daca ne uitam pe graficul functiei vedem ca $\frac{8}{15}$ $8/15$ (aproape $\frac{1}{2}$ $1/2$ ) reprezinta intersectia graficului cu axa $O x$ $Ox$ , deasupra careia, evident ca vom gasi doar valori pozitive.

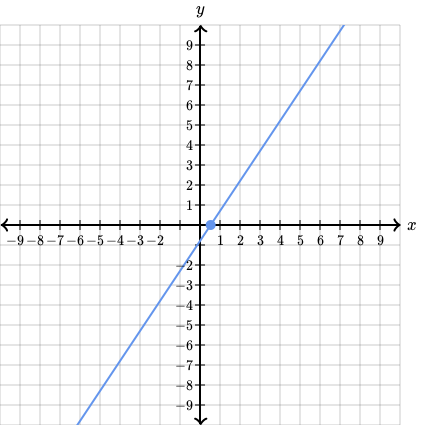
Dar acest punct reprezinta si locul unde functia isi schimba semnul, lucru despre care am discutat in lectia trecuta.

Asadar, solutia pentru inecuatia noastra $\frac{3}{2} \cdot x - \frac{4}{5} \geq 0$ $3/2*x - 4/5 >= 0$ , este intervalul care incepe din intersectia functiei cu axa $O x$ $Ox$ si continua catre $+ \infty$ $+infty$ , adica $(\frac{8}{15}, + \infty)$ $(8/15, +infty)$ .

Dar in mod general, toate solutiile pentru astfel de inegalitati incep dintr-un punct precum $\frac{8}{15}$ $8/15$ si continua catre $+ \infty$ $+infty$ sau $- \infty$ $-infty$ .

Putem deduce o definite mai generala, ca fiind:

Solutia unei inecuatii de forma $a \cdot x + b \geq 0$ $a*x + b ≥ 0$ (sau $\leq 0$ $≤ 0$ ) este intervalul ce incepe (sau se termina) cu $- \frac{b}{a}$ $-b/a$ dar este in functie de $a$ $a$ , dupa cum urmeaza:

$\begin{array}{l|c} \text{inegalitatea} & \class{text-blue}{\ge 0} & \class{text-red}{\le 0}\\ \hline \\ \class{text-blue}{a > 0} & \class{text-blue}{\left[-\frac{b}{a}, +\infty \right)} & \class{text-purple}{\left(-\infty, -\frac{b}{a} \right]} \\ \\ \class{text-red}{a < 0} & \class{text-purple}{\left(-\infty, -\frac{b}{a} \right]} & \class{text-red}{\left[-\frac{b}{a}, +\infty \right)} \end{array}$

Haideti sa luam urmatorul exemplu ca sa vedem exact cum folosim acest tabel.

Sa spunem ca avem functia $g (x) = - \frac{2}{3} \cdot x - 2$ $g(x) = - 2/3*x - 2$ si vrem sa aflam cand aceasta este $\leq 0$ $≤0$ .

$- \frac{2}{3} \cdot x - 2 \leq 0$ $- 2/3*x - 2 ≤ 0$

$- \frac{2}{3} \cdot x \leq 2$ $- 2/3*x ≤ 2$

si pentru ca $\class{text-red}{a}$ este mai mic decat $0$ $0$ , atunci cand vom inmulti cu inversul lui se va schimba semnul inegalitatii, si anume:

$(- \frac{3}{2}) \cdot (- \frac{2}{3}) \cdot x \geq 2 \cdot (- \frac{3}{2})$ $(- 3/2)*(- 2/3)*x >= 2*(- 3/2)$

$\Rightarrow x \geq - 3$ $rArr x >= -3$

Rezulta ca solutia este intervalul $\class{text-red}{\left[-3, +\infty \right)}$

Asadar conteaza semnul lui $a$ $a$ pentru ca acesta influenteaza semnul inegalitatii. El de asemenea este cel care ne spune daca graficul functiei este crescator sau descrescator. In acest caz este negativ, inseamna ca functia este descrescatoare, si asta se explica prin faptul ca pana intr-un punct vom gasi numere pozitive, si apoi numere negative. De aceea si solutia inegalitatii incepe dintr-un punct (in cazul nostru $- 3$ $-3$ ) si continua catre $+ \infty$ $+infty$ .

Aceasta se observa si din graficul functiei, pana in punctul $- 3$ $-3$ avem numere pozitive si apoi negative. Asadar putem afla solutia unei inecuatii si din graficul functiei.

De ce?

Cum calculam?

Rezulta ca solutia este intervalul [−3,+∞)[−3,+∞)\class{text-red}{\left[-3, +\infty \right)}

Rezulta ca solutia este intervalul $\class{text-red}{\left[-3, +\infty \right)}$