Inecuatii lineare

Stim ca o functie de gradul I are o ecuatie atasata. Dar in acelasi mod putem spune ca avem si o inecuatie pentru aceeasi functie.

De exemplu, pentru: $f (x) = 2 \cdot x + 5$ $f(x) = 2*x + 5$ avem ecuatia lineara: $2 \cdot x - y + 5 = 0$ $2*x - y + 5 = 0$ dar vom avea si inecuatia $2 \cdot x - y + 5 \leq 0$ $2*x - y + 5 ≤ 0$ (sau $\geq 0$ $>= 0$ ).

O inecuatie lineara ne arata regiunea din sistemul cartezian care cuprinde toate solutiile unei inecuatii de forma $a \cdot x + b \cdot y + c \geq 0$ $a*x + b*y +c >= 0$ (sau $\leq, <, >$ $≤, <, >$ decat 0)

Pentru o ecuatie lineara gaseam toate solutiile ei pe o dreapta. O inecuatie, care are aceeasi expresie, cuprinde regiunea superioara a graficului delimitata de dreapta, sau cea de sub grafic.

Ecuatia de mai devreme $2 \cdot x - y + 5 = 0$ $2*x - y + 5 = 0$ , are urmatorul grafic:

Iar graficul inecuatiei $2 \cdot x - y + 5 \leq 0$ $2*x - y + 5 ≤ 0$ , va cuprinde acea dreapta, dar si toata regiunea din grafic care este deasupra ei:

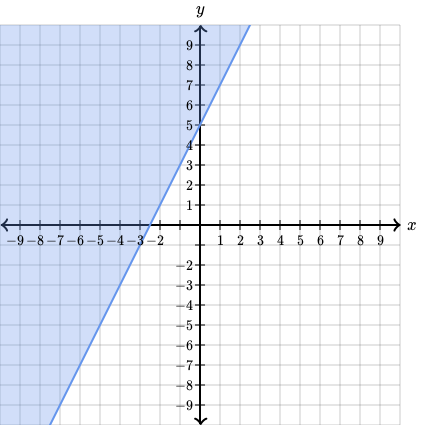
Iar daca am avea $2 \cdot x - y + 5 \geq 0$ $2*x - y + 5 >= 0$ , atunci ar fi fost vorba de regiunea de sub dreapta.

Si daca pare putin pe dos, putem sa pastram doar $y$ $y$ in partea stanga si sa ne gandim in functie de el.

$2 \cdot x - y + 5 \leq 0 \Rightarrow$ $2*x - y + 5 ≤ 0 =>$ $y \geq 2 \cdot x + 5$ $y >= 2*x + 5$

Astfel, daca avem $\geq$ $>=$ regiunea va fi deasupra dreptei, si daca avem $\leq$ $≤$ atunci este vorba de regiunea de sub dreapta.

Si putem testa daca aceasta este adevarata, luand un punct care stim ca se afla in acea regiune si apoi sa testam daca el chiar respecta inegalitatea.

De exemplu punctul $(\class{text-orange}{-3}, \class{text-purple}{6})$ se afla la stanga dreptei. Iar daca inlocuim in inegalitate ne rezulta ceva adevarat:

$2 \cdot (\class{text-orange}{-3}) - \class{text-purple}{6} + 5 \le 0$

$- 7 \leq 0$ $-7 ≤ 0$

Orice punct care se afla in acea regiune este o solutie pentru inecuatia noastra.

Asadar avem de un $\infty$ $infty$ mai multe solutii, pentru ca nu sunt doar punctele de pe dreapta, ci si toate punctele care se afla pe toate dreptele din acea regiune.

Daca am fi avut inecuatia doar cu semnul de $> 0$ $> 0$ , atunci ar fi fost vorba de aceleasi solutii dar mai putin cele de pe dreapta.